布隆过滤器(bloom filter)介绍以及php和redis实现布隆过滤器实现方法

引言

在介绍布隆过滤器之前我们首先引入几个场景。

场景一

在一个高并发的计数系统中，如果一个key没有计数，此时我们应该返回0。但是访问的key不存在，相当于每次访问缓存都不起作用了。那么如何避免频繁访问数量为0的key而导致的缓存被击穿？

有人说，将这个key的值置为0存入缓存不就行了吗？这是确实是一种解决方案。当访问一个不存在的key的时候，设置一个带有过期时间的标志，然后放入缓存。不过这样做的缺点也很明显：浪费内存和无法抵御随机key攻击。

场景二

在一个黑名单系统中，我们需要设置很多黑名单内容。比如一个邮件系统，我们需要设置黑名单用户，当判断垃圾邮件的时候，要怎么去做。比如爬虫系统，我们要记录下来已经访问过的链接避免下次访问重复的链接。

在邮件很少或者用户很少的情况下，我们用普通数据库自带的查询就能完成。在数据量太多的时候，为了保证速度，通常情况下我们会将结果缓存到内存中，数据结构用hash表。这种查找的速度是O(1)，但是内存消耗也是惊人的。打个比方，假如我们要存10亿条数据，每条数据平均占据32个字节，那么需要的内存是64G，这已经是一个惊人的大小了。

一种解决思路

能不能有一种思路，查询的速度是O(1)，消耗内存特别小呢？前辈门早就想出了一个很好的解决方案。由于上面说的场景判断的结果只有两种状态（是或者不是，存在或者不存在），那么对于所存的数据完全可以用位来表示。数据本身则可以通过一个hash函数计算出一个key，这个key是一个位置，而这个key所对的值就是0或者1（因为只有两种状态），如下图：

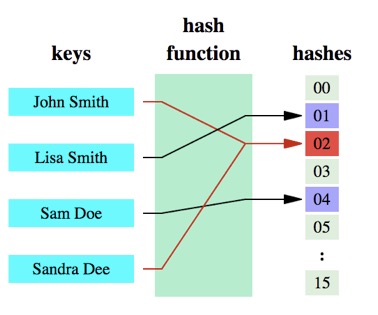
布隆过滤器原理

上面的思路其实就是布隆过滤器的思想，只不过因为hash函数的限制，多个字符串很可能会hash成一个值。为了解决这个问题，布隆过滤器引入多个hash函数来降低误判率。

下图表示有三个hash函数，比如一个集合中有x，y，z三个元素，分别用三个hash函数映射到二进制序列的某些位上，假设我们判断w是否在集合中，同样用三个hash函数来映射，结果发现取得的结果不全为1，则表示w不在集合里面。

布隆过滤器处理流程

布隆过滤器应用很广泛，比如垃圾邮件过滤，爬虫的url过滤，防止缓存击穿等等。下面就来说说布隆过滤器的一个完整流程，相信读者看到这里应该能明白布隆过滤器是怎样工作的。

第一步：开辟空间

开辟一个长度为m的位数组（或者称二进制向量），这个不同的语言有不同的实现方式，甚至你可以用文件来实现。

第二步：寻找hash函数

获取几个hash函数，前辈们已经发明了很多运行良好的hash函数，比如BKDRHash，JSHash，RSHash等等。这些hash函数我们直接获取就可以了。

第三步：写入数据

将所需要判断的内容经过这些hash函数计算，得到几个值，比如用3个hash函数，得到值分别是1000，2000，3000。之后设置m位数组的第1000，2000，3000位的值位二进制1。

第四步：判断

接下来就可以判断一个新的内容是不是在我们的集合中。判断的流程和写入的流程是一致的。

误判问题

布隆过滤器虽然很高效（写入和判断都是O(1)，所需要的存储空间极小），但是缺点也非常明显，那就是会误判。当集合中的元素越来越多，二进制序列中的1的个数越来越多的时候，判断一个字符串是否在集合中就很容易误判，原本不在集合里面的字符串会被判断在集合里面。

数学推导

布隆过滤器原理十分简单，但是hash函数个数怎么去判断，误判率有多少？

假设二进制序列有m位，那么经过当一个字符串hash到某一位的概率为：$\frac{1}{m}$。也就是说当前位被反转为1的概率：$p(1)=\frac{1}{m}$。那么这一位没有被反转的概率为：$p(0)=1-\frac{1}{m}$。

假设我们存入n各元素，使用k个hash函数，此时没有被翻转的概率为：$p(0)=(1-\frac{1}{m})^{nk}$。那什么情况下我们会误判呢，就是原本不应该被翻转的位，结果翻转了，也就是 $p(误判)=1-(1-\frac{1}{m})^{nk}$

由于只有k个hash函数同时误判了，整体才会被误判，最后误判的概率为 $p(误判)=(1-(1-\frac{1}{m})^{nk})^k$。

要使得误判率最低，那么我们需要求误判与m、n、k之间的关系，现在假设m和n固定，我们计算一下k。可以首先看看这个式子：$(1-\frac{1}{m})^{nk}$。

由于我们的m很大，通常情况下我们会用2^32来作为m的值。上面的式子中含有一个重要极限 $\lim\limits _{x\to\infty} (1+\frac{1}{x})^x = e$。

因此误判率的式子可以写成 $p(误判) = (1-(e)^{-nk/m})^k$。

接下来令$t = -n/m$，两边同时取对数，求导，得到：$p^{’} \frac{1}{p} = ln(1-e^{tk}) + \frac{ k lne^{t} (-e^{tk}) } {1-e^{tk}} $

让$p{’}=0$，则等式后面的为0，最后整理出来的结果是 $(1-e^{tk}) ln(1-e^{tk}) = e^{tk}lne^{tk} $

计算出来的k为$ln2\frac{m}{n}$，约等于$0.693\frac{m}{n}$，将k代入p(误判)，我们可以得到概率和m、n之间的关系，最后的结果 $(1/2)^{ln2 \frac{m}{n}}$，约等于$0.6185^{m/n}$

以上我们就得出了最佳hash函数个数以及误判率与mn之前的关系了。

下表是m与n比值在k个hash函数下面的误判率

m/n	k	k=1	k=2	k=3	k=4	k=5	k=6	k=7	k=8
2	1.39	0.393	0.400
3	2.08	0.283	0.237	0.253
4	2.77	0.221	0.155	0.147	0.160
5	3.46	0.181	0.109	0.092	0.092	0.101
6	4.16	0.154	0.0804	0.0609	0.0561	0.0578	0.0638
7	4.85	0.133	0.0618	0.0423	0.0359	0.0347	0.0364
8	5.55	0.118	0.0489	0.0306	0.024	0.0217	0.0216	0.0229
9	6.24	0.105	0.0397	0.0228	0.0166	0.0141	0.0133	0.0135	0.0145
10	6.93	0.0952	0.0329	0.0174	0.0118	0.00943	0.00844	0.00819	0.00846
11	7.62	0.0869	0.0276	0.0136	0.00864	0.0065	0.00552	0.00513	0.00509
12	8.32	0.08	0.0236	0.0108	0.00646	0.00459	0.00371	0.00329	0.00314
13	9.01	0.074	0.0203	0.00875	0.00492	0.00332	0.00255	0.00217	0.00199
14	9.7	0.0689	0.0177	0.00718	0.00381	0.00244	0.00179	0.00146	0.00129
15	10.4	0.0645	0.0156	0.00596	0.003	0.00183	0.00128	0.001	0.000852
16	11.1	0.0606	0.0138	0.005	0.00239	0.00139	0.000935	0.000702	0.000574
17	11.8	0.0571	0.0123	0.00423	0.00193	0.00107	0.000692	0.000499	0.000394
18	12.5	0.054	0.0111	0.00362	0.00158	0.000839	0.000519	0.00036	0.000275
19	13.2	0.0513	0.00998	0.00312	0.0013	0.000663	0.000394	0.000264	0.000194
20	13.9	0.0488	0.00906	0.0027	0.00108	0.00053	0.000303	0.000196	0.00014
21	14.6	0.0465	0.00825	0.00236	0.000905	0.000427	0.000236	0.000147	0.000101
22	15.2	0.0444	0.00755	0.00207	0.000764	0.000347	0.000185	0.000112	7.46e-05
23	15.9	0.0425	0.00694	0.00183	0.000649	0.000285	0.000147	8.56e-05	5.55e-05
24	16.6	0.0408	0.00639	0.00162	0.000555	0.000235	0.000117	6.63e-05	4.17e-05
25	17.3	0.0392	0.00591	0.00145	0.000478	0.000196	9.44e-05	5.18e-05	3.16e-05
26	18	0.0377	0.00548	0.00129	0.000413	0.000164	7.66e-05	4.08e-05	2.42e-05
27	18.7	0.0364	0.0051	0.00116	0.000359	0.000138	6.26e-05	3.24e-05	1.87e-05
28	19.4	0.0351	0.00475	0.00105	0.000314	0.000117	5.15e-05	2.59e-05	1.46e-05
29	20.1	0.0339	0.00444	0.000949	0.000276	9.96e-05	4.26e-05	2.09e-05	1.14e-05
30	20.8	0.0328	0.00416	0.000862	0.000243	8.53e-05	3.55e-05	1.69e-05	9.01e-06
31	21.5	0.0317	0.0039	0.000785	0.000215	7.33e-05	2.97e-05	1.38e-05	7.16e-06
32	22.2	0.0308	0.00367	0.000717	0.000191	6.33e-05	2.5e-05	1.13e-05	5.73e-06

php+Redis实现的布隆过滤器

由于Redis实现了setbit和getbit操作，天然适合实现布隆过滤器，redis也有布隆过滤器插件。这里使用php+redis实现布隆过滤器。

首先定义一个hash函数集合类，这些hash函数不一定都用到，实际上32位hash值的用3个就可以了，具体的数量可以根据你的位序列总量和你需要存入的量决定，上面已经给出最佳值。

class BloomFilterHash
{
	/**
	 * 由Justin Sobel编写的按位散列函数
	 */
	public function JSHash($string, $len = null)
	{
    	$hash = 1315423911;
    	$len || $len = strlen($string);
    	for ($i=0; $i<$len; $i++) {
    		$hash ^= (($hash << 5) + ord($string[$i]) + ($hash >> 2));
    	}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}

	/**
	 * 该哈希算法基于AT＆T贝尔实验室的Peter J. Weinberger的工作。
	 * Aho Sethi和Ulman编写的“编译器（原理，技术和工具）”一书建议使用采用此特定算法中的散列方法的散列函数。
	 */
	public function PJWHash($string, $len = null)
	{
		$bitsInUnsignedInt = 4 * 8; //（unsigned int）（sizeof（unsigned int）* 8）;
    	$threeQuarters = ($bitsInUnsignedInt * 3) / 4;
    	$oneEighth = $bitsInUnsignedInt / 8;
    	$highBits = 0xFFFFFFFF << (int) ($bitsInUnsignedInt - $oneEighth);
    	$hash = 0;
    	$test = 0;
    	$len || $len = strlen($string);
    	for($i=0; $i<$len; $i++) {
			$hash = ($hash << (int) ($oneEighth)) + ord($string[$i]); } $test = $hash & $highBits; if ($test != 0) { $hash = (($hash ^ ($test >> (int)($threeQuarters))) & (~$highBits));
    	}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}

	/**
	 * 类似于PJW Hash功能，但针对32位处理器进行了调整。它是基于UNIX的系统上的widley使用哈希函数。
	 */
	public function ELFHash($string, $len = null)
	{
		$hash = 0;
		$len || $len = strlen($string);
    	for ($i=0; $i<$len; $i++) {
        	$hash = ($hash << 4) + ord($string[$i]); $x = $hash & 0xF0000000; if ($x != 0) { $hash ^= ($x >> 24);
        	}
        	$hash &= ~$x;
    	}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}

	/**
	 * 这个哈希函数来自Brian Kernighan和Dennis Ritchie的书“The C Programming Language”。
	 * 它是一个简单的哈希函数，使用一组奇怪的可能种子，它们都构成了31 .... 31 ... 31等模式，它似乎与DJB哈希函数非常相似。
	 */
	public function BKDRHash($string, $len = null)
	{
    	$seed = 131;  # 31 131 1313 13131 131313 etc..
    	$hash = 0;
    	$len || $len = strlen($string);
    	for ($i=0; $i<$len; $i++) {
        	$hash = (int) (($hash * $seed) + ord($string[$i]));
    	}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}

	/**
	 * 这是在开源SDBM项目中使用的首选算法。
	 * 哈希函数似乎对许多不同的数据集具有良好的总体分布。它似乎适用于数据集中元素的MSB存在高差异的情况。
	 */
	public function SDBMHash($string, $len = null)
	{
		$hash = 0;
		$len || $len = strlen($string);
		for ($i=0; $i<$len; $i++) {
			$hash = (int) (ord($string[$i]) + ($hash << 6) + ($hash << 16) - $hash);
		}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}

	/**
	 * 由Daniel J. Bernstein教授制作的算法，首先在usenet新闻组comp.lang.c上向世界展示。
	 * 它是有史以来发布的最有效的哈希函数之一。
	 */
	public function DJBHash($string, $len = null)
	{
		$hash = 5381;
		$len || $len = strlen($string);
		for ($i=0; $i<$len; $i++) {
			$hash = (int) (($hash << 5) + $hash) + ord($string[$i]);
		}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}

	/**
	 * Donald E. Knuth在“计算机编程艺术第3卷”中提出的算法，主题是排序和搜索第6.4章。
	 */
	public function DEKHash($string, $len = null)
	{
		$len || $len = strlen($string);
		$hash = $len;
		for ($i=0; $i<$len; $i++) {
			$hash = (($hash << 5) ^ ($hash >> 27)) ^ ord($string[$i]);
		}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}

	/**
	 * 参考 http://www.isthe.com/chongo/tech/comp/fnv/
	 */
	public function FNVHash($string, $len = null)
	{
		$prime = 16777619; //32位的prime 2^24 + 2^8 + 0x93 = 16777619
		$hash = 2166136261; //32位的offset
		$len || $len = strlen($string);
		for ($i=0; $i<$len; $i++) {
			$hash = (int) ($hash * $prime) % 0xFFFFFFFF;
			$hash ^= ord($string[$i]);
		}
		return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
	}
}

接着就是连接redis来进行操作

/**
 * 使用redis实现的布隆过滤器
 */
abstract class BloomFilterRedis
{
	/**
	 * 需要使用一个方法来定义bucket的名字
	 */
	protected $bucket;

	protected $hashFunction;

	public function __construct($config, $id)
	{
		if (!$this->bucket || !$this->hashFunction) {
			throw new Exception("需要定义bucket和hashFunction", 1);
		}
		$this->Hash = new BloomFilterHash;
		$this->Redis = new YourRedis; //假设这里你已经连接好了
	}

	/**
	 * 添加到集合中
	 */
	public function add($string)
	{
		$pipe = $this->Redis->multi();
		foreach ($this->hashFunction as $function) {
			$hash = $this->Hash->$function($string);
			$pipe->setBit($this->bucket, $hash, 1);
		}
		return $pipe->exec();
	}

	/**
	 * 查询是否存在, 如果曾经写入过，必定回true，如果没写入过，有一定几率会误判为存在
	 */
	public function exists($string)
	{
		$pipe = $this->Redis->multi();
		$len = strlen($string);
		foreach ($this->hashFunction as $function) {
			$hash = $this->Hash->$function($string, $len);
			$pipe = $pipe->getBit($this->bucket, $hash);
		}
		$res = $pipe->exec();
		foreach ($res as $bit) {
			if ($bit == 0) {
				return false;
			}
		}
		return true;
	}

}

上面定义的是一个抽象类，如果要使用，可以根据具体的业务来使用。比如下面是一个过滤重复内容的过滤器。

/**
 * 重复内容过滤器
 * 该布隆过滤器总位数为2^32位, 判断条数为2^30条. hash函数最优为3个.(能够容忍最多的hash函数个数)
 * 使用的三个hash函数为
 * BKDR, SDBM, JSHash
 *
 * 注意, 在存储的数据量到2^30条时候, 误判率会急剧增加, 因此需要定时判断过滤器中的位为1的的数量是否超过50%, 超过则需要清空.
 */
class FilteRepeatedComments extends BloomFilterRedis
{
	/**
	 * 表示判断重复内容的过滤器
	 * @var string
	 */
	protected $bucket = 'rptc';

	protected $hashFunction = array('BKDRHash', 'SDBMHash', 'JSHash');
}

你可能还喜欢下面这些文章

gcc/g++编译参数详解

编译步骤gcc 与 g++ 分别是 gnu 的 c & c++ 编译器。gcc/g++ 在执行编译工作的时候，总共需要4步：预处理,生成 .i 的文件将预处理后的文件转换成汇编语言, 生成文件 .s 有汇编变为目标代码(机器代码)生成 .o 的文件连接目标代码, 生成可执行程序参数详解-x language filename参数含义为指定文件所使用的语言。根据约定，C语言的后缀名称为".c"，而 C++ 的后缀名为".cpp"或".cc"，但如果你的源代码后缀不约定的那几种，那么需要使用-x参数来指定文件所使用的语言。这个参数对他后面的文件名都起作用。可以使用的参数吗有下面的这些：

iterm2 使用 rz、sz 的方法

如果没有额外的设置，iterm2 使用 rzsz 的时候会卡在这个时候就需要使用iterm2提供的trigger来实现rzsz的功能。第一步：本机安装rzsz使用rzsz之前本地也需要安装如果没有安装brew，请先安装brew，mac必备的包管理器！第二步：创建发送和接收脚本发送文件的脚本如下，可以复制下面的内容，保存在 /usr/local/bin/iterm2-send-zmodem.sh中。接收文件的脚本如下，同样可以复制保存在/usr/local/bin/iterm2-recv-zmodem.sh第三步：设置Triggerteigger需要设置两个，一个实发送文件的trigger，一个

使用sublime+platuml高效画图

程序员难免要经常画流程图，状态图，时序图等。以前经常用 visio 画，经常为矩形画多大，摆放在哪等问题费脑筋。有时候修改文字后，为了较好的显示效果不得不再去修改图形。今天介绍的工具是如何使用 Sublime + PlantUML 的插件画流程图，状态图，时序图等。这是一种程序员看了就会爱上的画图方式：自然，高效。什么是 PlantUMLPlantUML 是一个画图脚本语言，用它可以快速地画出：时序图流程图用例图状态图组件图简单地讲，我们使用 visio 画图时需要一个一个图去画，但使用 PlantUML 只需要用文字表达出图的内容，然后就可以直接生成图片。看一个最简单的例子：软件安装这些软件

Go入门：六、常用标准库

这是我的Go学习的第六篇笔记，也是Go入门的最后一篇笔记。在大多数语言中，了解了变量和数据类型，流程控制，函数，面向对象，再加上标准库，就可以用这门语言去写一些项目了。首先让我想想，在工作中通常会用语言频繁处理什么问题或者处理什么数据？最常见的应该是各种字符串操作，日期和时间，读写文件、socket等IO相关的操作！字符串处理 — StringsString提供了一组处理字符串的操作，常用的有：判断一个字符串是否在另一个字符串中分割字符串为[]string和组合[]string为一个字符串字符串替换...太多了，就不一一列举了，这里列出一些常用的字符串操作。字符串判断字符串分割与合并字符串转换

Go入门：四、面向对象

这是我的Go学习笔记的第四篇，面向对象！现代语言几乎都会面向对象进行了支持！当然，Go也具备面向对象的特性！我的语言学习过程一般分为下面几个：1. 变量和数据类型2. 流程控制方法3. 函数声明和调用4. 面向对象5. 语言特性6. 标准库Go语言中的面向对象有点特殊。在Go语言里面，没有显式的class、extends等面向对象语言经常使用的关键词，但是却有面向对象的特性。看看Go怎么实现的把！创建一个类按照我的理解，类实际上就是某种模板，这个模板里面含有有限多个属性和方法。在Go里面，定义这个模板的语法使用type来实现！比如单个int类型可以构成一个类（没错，你甚至可以在int数据类型上

signal函数详解

signal作用是为信号注册一个处理器。这里的“信号”是软中断信号，这种信号来源主要有三种：程序错误：比如除0，非法内存访问。外部信号：终端Ctrl-C产生的SIGINT信号，定时器产生的SIGALERM。显示请求：kill函数发送的任意信号。当kill一个进程的时候，默认会发送SIGTERM信号，此时这个信号只有默认处理操作（SIG_DFL），直接中断进程执行。如果此时该进程正在执行一个任务，直接终止该进程会导致任务没有完成。这个时候为SIGTERM信号注册一个信号处理函数就十分有必要。介绍参数sig要设置信号处理函数的信号。它可以是实现定义值或下例值之一：SIGABRTSIGFPESIGI

C++动态内存管理

C++中，动态内存管理是通过一对运算符来完成：new 和 delete。new操作符在内存中为对象分配空间并返回一个指向该对象的指针，delete接收一个动态对象的指针，销毁该对象，并释放与之相关的内存。手动管理内存看起来只有这两个操作，似乎很轻松，但实际上这是一件非常繁琐的事情，分配了内存但没有释放内存的场景发生的概率太大了！回想一下，你有多少次打开抽屉却没关上，拿出来的护肤品擦完脸之后却忘了放回去，吃完饭却忘了洗碗。类似这种没有收尾的事情我做的太多了。（以上这些都是在实际生活中我爱人批评我的点）我连这种明面上的事情都能忘记收尾，何况分配内存！所以为了世界和平，我放弃了手动管理内存。好在C+

C++右值引用和移动

Attention：this blog is a translation of https://www.internalpointers.com/post/c-rvalue-references-and-move-semantics-beginners ,which is posted by @internalpoiners.一、前言在我的前一篇文章里，我解释了右值背后的逻辑。核心的思想就是：在C++中你总会有一些临时的、生命周期较短的值，这些值无论如何你都无法改变。令人惊喜的是，现代C++（通常指C++0x或者更高的版本）引入了右值引用（rvalue reference）的概念：它是一个新的

C++入门：三、函数

这是我学习C++的第三篇笔记，函数。我的学习路径是现在学习的是函数的声明、定义、调用等相关知识。函数声明和定义函数的声明包含返回类型，函数名字，0个或者多个形参，无函数体，通常在头文件中对函数进行声明。函数的定义包含返回类型，函数名字，0个或多个形参，以及函数体。比如写一个求阶乘的函数，可以写成下面这样写一些简单的函数大多数语言都差不多，不过可惜每种语言或多或少都有自己的特色，这是比较令人头秃的地方。函数的参数函数可以带有0或多个参数，每个参数都需要声明类型。参数传递可以传值和传引用。如果形参是引用类型，那么它将绑定到对应的实参中，我们成为传引用。否则，将会把实参的值拷贝后赋值给形参，我们成为

如何选择特征

特征工程是数据分析中最耗时间和精力的一部分工作，它不像算法和模型那样是确定的步骤，更多是工程上的经验和权衡。因此没有统一的方法。这里只是对一些常用的方法做一个总结。本文关注于特征选择部分。后面还有两篇会关注于特征表达和特征预处理。1. 特征的来源在做数据分析的时候，特征的来源一般有两块，一块是业务已经整理好各种特征数据，我们需要去找出适合我们问题需要的特征；另一块是我们从业务特征中自己去寻找高级数据特征。我们就针对这两部分来分别讨论。2. 选择合适的特征我们首先看当业务已经整理好各种特征数据时，我们如何去找出适合我们问题需要的特征，此时特征数可能成百上千，哪些才是我们需要的呢？第一

赞赏

微信赞赏支付宝赞赏