数据结构

引言

在介绍布隆过滤器之前我们首先引入几个场景。

场景一

在一个高并发的计数系统中，如果一个key没有计数，此时我们应该返回0。但是访问的key不存在，相当于每次访问缓存都不起作用了。那么如何避免频繁访问数量为0的key而导致的缓存被击穿？

有人说，将这个key的值置为0存入缓存不就行了吗？这是确实是一种解决方案。当访问一个不存在的key的时候，设置一个带有过期时间的标志，然后放入缓存。不过这样做的缺点也很明显：浪费内存和无法抵御随机key攻击。

场景二

在一个黑名单系统中，我们需要设置很多黑名单内容。比如一个邮件系统，我们需要设置黑名单用户，当判断垃圾邮件的时候，要怎么去做。比如爬虫系统，我们要记录下来已经访问过的链接避免下次访问重复的链接。

在邮件很少或者用户很少的情况下，我们用普通数据库自带的查询就能完成。在数据量太多的时候，为了保证速度，通常情况下我们会将结果缓存到内存中，数据结构用hash表。这种查找的速度是O(1)，但是内存消耗也是惊人的。打个比方，假如我们要存10亿条数据，每条数据平均占据32个字节，那么需要的内存是64G，这已经是一个惊人的大小了。

一种解决思路

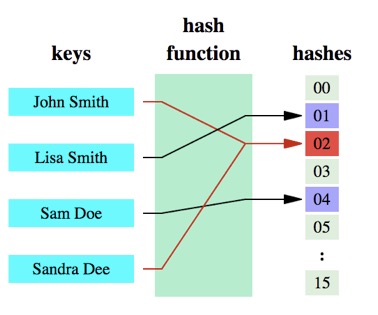
能不能有一种思路，查询的速度是O(1)，消耗内存特别小呢？前辈门早就想出了一个很好的解决方案。由于上面说的场景判断的结果只有两种状态（是或者不是，存在或者不存在），那么对于所存的数据完全可以用位来表示。数据本身则可以通过一个hash函数计算出一个key，这个key是一个位置，而这个key所对的值就是0或者1（因为只有两种状态），如下图：

（更多…）

你可能还喜欢下面这些文章

gcc/g++编译参数详解

编译步骤gcc 与 g++ 分别是 gnu 的 c & c++ 编译器。gcc/g++ 在执行编译工作的时候，总共需要4步：预处理,生成 .i 的文件将预处理后的文件转换成汇编语言, 生成文件 .s 有汇编变为目标代码(机器代码)生成 .o 的文件连接目标代码, 生成可执行程序参数详解-x language filename参数含义为指定文件所使用的语言。根据约定，C语言的后缀名称为".c"，而 C++ 的后缀名为".cpp"或".cc"，但如果你的源代码后缀不约定的那几种，那么需要使用-x参数来指定文件所使用的语言。这个参数对他后面的文件名都起作用。可以使用的参数吗有下面的这些：

iterm2 使用 rz、sz 的方法

如果没有额外的设置，iterm2 使用 rzsz 的时候会卡在这个时候就需要使用iterm2提供的trigger来实现rzsz的功能。第一步：本机安装rzsz使用rzsz之前本地也需要安装如果没有安装brew，请先安装brew，mac必备的包管理器！第二步：创建发送和接收脚本发送文件的脚本如下，可以复制下面的内容，保存在 /usr/local/bin/iterm2-send-zmodem.sh中。接收文件的脚本如下，同样可以复制保存在/usr/local/bin/iterm2-recv-zmodem.sh第三步：设置Triggerteigger需要设置两个，一个实发送文件的trigger，一个

使用sublime+platuml高效画图

程序员难免要经常画流程图，状态图，时序图等。以前经常用 visio 画，经常为矩形画多大，摆放在哪等问题费脑筋。有时候修改文字后，为了较好的显示效果不得不再去修改图形。今天介绍的工具是如何使用 Sublime + PlantUML 的插件画流程图，状态图，时序图等。这是一种程序员看了就会爱上的画图方式：自然，高效。什么是 PlantUMLPlantUML 是一个画图脚本语言，用它可以快速地画出：时序图流程图用例图状态图组件图简单地讲，我们使用 visio 画图时需要一个一个图去画，但使用 PlantUML 只需要用文字表达出图的内容，然后就可以直接生成图片。看一个最简单的例子：软件安装这些软件

Go入门：六、常用标准库

这是我的Go学习的第六篇笔记，也是Go入门的最后一篇笔记。在大多数语言中，了解了变量和数据类型，流程控制，函数，面向对象，再加上标准库，就可以用这门语言去写一些项目了。首先让我想想，在工作中通常会用语言频繁处理什么问题或者处理什么数据？最常见的应该是各种字符串操作，日期和时间，读写文件、socket等IO相关的操作！字符串处理 — StringsString提供了一组处理字符串的操作，常用的有：判断一个字符串是否在另一个字符串中分割字符串为[]string和组合[]string为一个字符串字符串替换...太多了，就不一一列举了，这里列出一些常用的字符串操作。字符串判断字符串分割与合并字符串转换

Go入门：四、面向对象

这是我的Go学习笔记的第四篇，面向对象！现代语言几乎都会面向对象进行了支持！当然，Go也具备面向对象的特性！我的语言学习过程一般分为下面几个：1. 变量和数据类型2. 流程控制方法3. 函数声明和调用4. 面向对象5. 语言特性6. 标准库Go语言中的面向对象有点特殊。在Go语言里面，没有显式的class、extends等面向对象语言经常使用的关键词，但是却有面向对象的特性。看看Go怎么实现的把！创建一个类按照我的理解，类实际上就是某种模板，这个模板里面含有有限多个属性和方法。在Go里面，定义这个模板的语法使用type来实现！比如单个int类型可以构成一个类（没错，你甚至可以在int数据类型上

signal函数详解

signal作用是为信号注册一个处理器。这里的“信号”是软中断信号，这种信号来源主要有三种：程序错误：比如除0，非法内存访问。外部信号：终端Ctrl-C产生的SIGINT信号，定时器产生的SIGALERM。显示请求：kill函数发送的任意信号。当kill一个进程的时候，默认会发送SIGTERM信号，此时这个信号只有默认处理操作（SIG_DFL），直接中断进程执行。如果此时该进程正在执行一个任务，直接终止该进程会导致任务没有完成。这个时候为SIGTERM信号注册一个信号处理函数就十分有必要。介绍参数sig要设置信号处理函数的信号。它可以是实现定义值或下例值之一：SIGABRTSIGFPESIGI

C++动态内存管理

C++中，动态内存管理是通过一对运算符来完成：new 和 delete。new操作符在内存中为对象分配空间并返回一个指向该对象的指针，delete接收一个动态对象的指针，销毁该对象，并释放与之相关的内存。手动管理内存看起来只有这两个操作，似乎很轻松，但实际上这是一件非常繁琐的事情，分配了内存但没有释放内存的场景发生的概率太大了！回想一下，你有多少次打开抽屉却没关上，拿出来的护肤品擦完脸之后却忘了放回去，吃完饭却忘了洗碗。类似这种没有收尾的事情我做的太多了。（以上这些都是在实际生活中我爱人批评我的点）我连这种明面上的事情都能忘记收尾，何况分配内存！所以为了世界和平，我放弃了手动管理内存。好在C+

C++右值引用和移动

Attention：this blog is a translation of https://www.internalpointers.com/post/c-rvalue-references-and-move-semantics-beginners ,which is posted by @internalpoiners.一、前言在我的前一篇文章里，我解释了右值背后的逻辑。核心的思想就是：在C++中你总会有一些临时的、生命周期较短的值，这些值无论如何你都无法改变。令人惊喜的是，现代C++（通常指C++0x或者更高的版本）引入了右值引用（rvalue reference）的概念：它是一个新的

C++入门：三、函数

这是我学习C++的第三篇笔记，函数。我的学习路径是现在学习的是函数的声明、定义、调用等相关知识。函数声明和定义函数的声明包含返回类型，函数名字，0个或者多个形参，无函数体，通常在头文件中对函数进行声明。函数的定义包含返回类型，函数名字，0个或多个形参，以及函数体。比如写一个求阶乘的函数，可以写成下面这样写一些简单的函数大多数语言都差不多，不过可惜每种语言或多或少都有自己的特色，这是比较令人头秃的地方。函数的参数函数可以带有0或多个参数，每个参数都需要声明类型。参数传递可以传值和传引用。如果形参是引用类型，那么它将绑定到对应的实参中，我们成为传引用。否则，将会把实参的值拷贝后赋值给形参，我们成为

如何选择特征

特征工程是数据分析中最耗时间和精力的一部分工作，它不像算法和模型那样是确定的步骤，更多是工程上的经验和权衡。因此没有统一的方法。这里只是对一些常用的方法做一个总结。本文关注于特征选择部分。后面还有两篇会关注于特征表达和特征预处理。1. 特征的来源在做数据分析的时候，特征的来源一般有两块，一块是业务已经整理好各种特征数据，我们需要去找出适合我们问题需要的特征；另一块是我们从业务特征中自己去寻找高级数据特征。我们就针对这两部分来分别讨论。2. 选择合适的特征我们首先看当业务已经整理好各种特征数据时，我们如何去找出适合我们问题需要的特征，此时特征数可能成百上千，哪些才是我们需要的呢？第一

树

树是一种层次关系，在日常生活非常常见，比如社会关系，亲缘关系，文件管理。

一棵树是一些节点的集合，这个集合可以是空集，若非空，则一棵树由称作为根的节点r以及0个或者多个非空的（子）树组成，这些子树中的每一棵都是被来自根r的一条有向的边所连接。

一种数据结构需要包含一些操作，树这种数据结构有增加，删除，查找，修改。

节点

节点的度：节点子树的个数。

叶子节点：没有儿子的节点，也就是度为0的节点。

节点的层次：规定跟节点在1层，其他节点的层次为父节点的层次加1。

节点的高：节点的高为从这个节点到叶子的最长路径，所有树叶的高都是0。

节点的深度：从跟节点到该节点的唯一路径长，根的深度为0。

节点定义

typedef struct TreeNode *PtrToNode;

struct TreeNode
{
    ElementType Element;
    PtrToNode FitstChild;
    PtrNode NextSibling;
}

（更多…）

你可能还喜欢下面这些文章

一致性哈希的php实现

未来项目可能要上memcache集群，memcache集群的key分配完全在客户端完成，服务端不做任何处理，这里对key进行分配节点的最优方式就是使用一致性哈希。记得以前用mysql进行分库分表的时候，通常会用一个求余作为哈希函数，这样一些id就能对应相应的表了。不过使用mysql的时候，我们不需要考虑这些节点失效问题，以及节点增加或者减少的问题（在此之前应该做好足够的计划和准备），但是对于缓存，通常就比较宽松了，允许节点失效问题，但是普通的hash分配在节点失效之后，大部分的缓存位置都改变了，这显然个灾难，这个时候就要考虑一致性hash了，在增加或者删除节点，只有小部分的key会受影响。一致

使用php curl 的并发能力可以做什么

在php中，没有多线程让编程变得简单。但在一些需要并发提升性能的场景下，显得有些无能为力，比如发起一些http请求。但好在curl扩展可以让我们“并发”去请求网络资源。利用这个特点，我们能做很多有趣的事情。最基础的，并发请求网络资源，提升处理速度。并发访问代码<?phpclass ConcurrencyHTTP { private $_requests; private $_callbacks; private $_currentIndex = 0; public function get($url, $header = array(), $timeout = 3

shell中map的使用

bash 4.1.2 版本增加了map数据结构。map是一种常用的数据结构，通过map可以将key映射到一个value。使用方法map在使用之前需要先声明，声明的方式如下map需要先声明再使用。参数-A表示声明的变量是一个map。需要注意的是这里的A是大写的字母A。赋值操作map的赋值有两种方式，一种是直接给map赋值，如下：另一种是使用下标给map添加key-value对输出所有的key在文中最开始提到map的使用需要先声明，在没有声明的情况下此处会输出一个0，如下图：输出所有value输出map长度遍历，根据key找到对应的value遍历所有的key遍历所有的value问题FAQQ：为什么

介绍一款工具，memcacheadmin，使用php制作的memcached管理监控工具

MemAdmin是一款可视化的Memcached管理与监控工具，使用PHP开发，体积小，操作简单。主要功能：服务器参数监控：STATS、SETTINGS、ITEMS、SLABS、SIZES实时刷新服务器性能监控：GET、DELETE、INCR、DECR、CAS等常用操作命中率实时监控支持数据遍历，方便对存储内容进行监视支持条件查询，筛选出满足条件的KEY或VALUE 数组、JSON等序列化字符反序列显示兼容memcache协议的其他服务，如Tokyo Tyrant (遍历功能除外) 支持服务器连接池，多服务器管理切换方便简洁guthub地址：https://github.com/ju

c++ 标准库二分查找

C++标准库中的二分查找可以通过和函数实现。这两个函数都在头文件中定义，并接受一个排序的范围（例如，，，等）以及一个要查找的值。返回指向在范围中第一个不小于（即大于或等于）给定值的元素的迭代器。则返回指向在范围中第一个大于给定值的元素的迭代器。下面是一个使用进行二分查找的例子：在这个例子中，我们首先定义了一个排序的，然后定义了一个目标值。我们使用查找，然后检查返回的迭代器是否指向。如果是，我们就打印出在中的位置。否则，我们打印出未找到的消息。如果你想查找的是范围中是否包含特定的值，并且不关心具体的位置，你可以将和的结果进行比较。如果它们相同，那么范围中不包含该值。否则，范围中包含该值。请注意，

mongo读写分离的一些坑

在使用mongo副本集的时候就在想，这些副本不用来读太浪费了，再翻阅php的mongodb驱动，发现一个美好的readPreference，可以设定读取的优先级，其中就有优先读取副本，甚至还可以设定读取最小网络延迟的节点，具体可以参考：http://php.net/manual/zh/mongodb-driver-readpreference.construct.php愿望是美好的，然而使用的过程中当我优先读取secondary时候，经常发现有的读取时间在几秒甚至几十秒的情况，也是醉了。于是经过一番搜索，发现有一个博客提到了这个问题，在官方文档中有说明，原文如下:How does concur

命令行下的mongo初试

从连接mongo开始，熟悉一下命令行下面的mongo使用连接普通连接mongo mongodb://ip:port查看数据库show dbs选择或者创建数据库use mydb创建一个集合比如创建一个mycollection的集合db.createCollection('mycollection')显示数据库中所有的集合show collections向集合中写入数据假设我们创建了一个mycollection集合，实际上当我们没有创建mycollection集合的时候，执行下面的命令mongo会自动创建一个mycollection集合db.mycollection.insert({"foo",'

python学习笔记：二、流程控制

根据如何学习一门新的语言这篇文章的指导，现在的步骤就是学习这门语言的流程控制了。通常来讲，流程控制有顺序，选择，循环这几种。python也不例外，也有这三种流程控制。下面的一一学习。顺序顺序语句很简单，从上往下依次顺序执行。如：a = 1b = 2print(a+b)上面的语句就是顺序执行的语句。选择选择通常使用if和switch，但python中只有if这一个选择语句。语法是：if 满足条件1: 语句1elif 不满足条件1满足1条件2 语句2else 都不满足语句3比如用一个实际的例子a = 1b = 2if a > b: print('a>b')el

布隆过滤器(bloom filter)介绍以及php和redis实现布隆过滤器实现方法

引言

数据结构学习笔记：树

树

节点